An annotatable worksheet for this presentation is available as Worksheet 11 .
In this section we will explore digital systems and learn more about the z-transfer function model.
The material in this presentation and notes is based on Chapter 9 (Starting at Section 9.7) of [Karris, 2012] . I have skipped the section on digital state-space models.
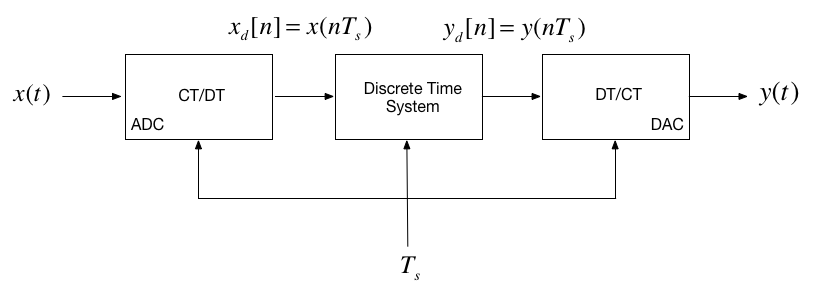
In the lecture that introduced the z-transform we talked about the representation of a discrete-time (DT) system by the model shown below:

In this session, we want to explore the contents of the central block.

Let us assume that the sequence transformation is a difference equation of the form 2 :
From the z-transform properties
\[f[n-m] \Leftrightarrow z^<-m>F(z)\] \[Y(z) + a_1z^<-1>Y(z) + a_2z^Y(z) + \cdots + a_kz^Y(z) = . \] \[b_0 U(z) + b_1z^<-1>U(z) + b_2z^U(z) + \cdots + b_kz^U(z)\]\[\begin
We define the discrete time transfer function \(H(z) := Y(z)/U(z)\) so…
\[H(z) = \frac = \fracz^ + b_z^ + \cdots b_z^>z^ + a_z^ + \cdots a_z^ >\]… or more conventionally 3 :
\[H(z) = \fracz^ + b_z^ + \cdots b_z + b_>z^ + a_z^ + \cdots a_ z + a_>\]The discrete-time impulse reponse \(h[n]\) is the response of the DT system to the input \(x[n] = \delta[n]\)
Last week we showed that
\[\mathcalwas defined by the transform pair
\[\delta[n] \Leftrightarrow 1\] \[h[n] = \mathcalWe will work through an example in class.
[Skip next slide in Pre-Lecture]
Karris Example 9.10:
The difference equation describing the input-output relationship of a DT system with zero initial conditions, is:
\[y[n] - 0.5 y[n-1] + 0.125 y[n-2] = x[n] + x[n -1]\]clear all cd matlab pwd format compact open dtm_ex1_2
ans = '/Users/eechris/code/src/github.com/cpjobling/eg-247-textbook/dt_systems/4/matlab'
The difference equation describing the input-output relationship of the DT system with zero initial conditions, is:
\[y[n] - 0.5 y[n-1] + 0.125 y[n-2] = x[n] + x[n -1]\]Numerator \(z^2 + z\)
Nz = [1 1 0];
Denominator \(z^2 - 0.5 z + 0.125\)
Dz = [1 -0.5 0.125];
[r,p,k] = residue(Nz,Dz)
r = 0.7500 - 0.5000i 0.7500 + 0.5000i
p = 0.2500 + 0.2500i 0.2500 - 0.2500i k = 1
Hz = tf(Nz,Dz,1) hn = impulse(Hz, 15);
z^2 + z
z^2 - 0.5 z + 0.125
Sample time: 1 seconds
Discrete-time transfer function.
stem([0:15], hn) grid title('Example 5 - Part 2') xlabel('n') ylabel('Impulse response h[n]')
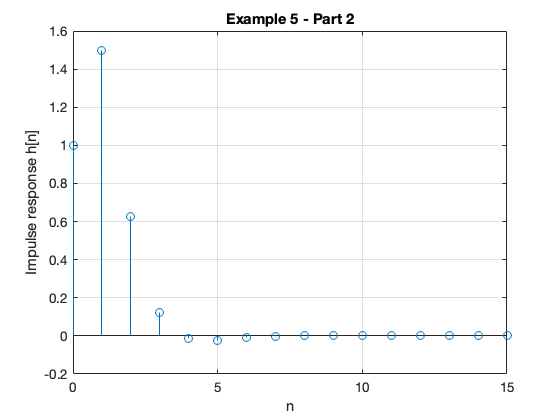
impulse(Hz,15) grid title('Example 5 - Part 2 - As Analogue Signal') xlabel('nTs [s]') ylabel('Impulse response h(t)')

We will work through this example in class.
[Skip next slide in Pre-Lecture]
\[\beginSolved by inverse Z-transform.
open dtm_ex1_3
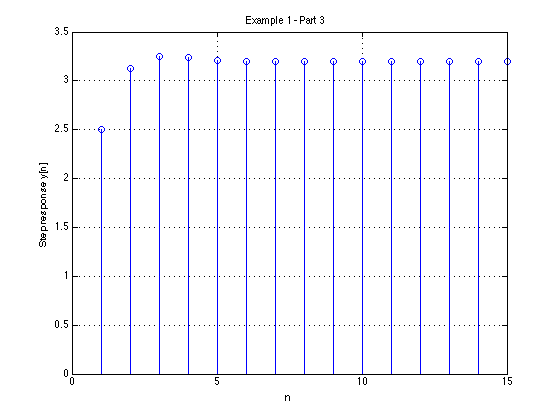
We will consider some examples in class
Code extracted from dtm_ex1_3.m:
Ts = 1; z = tf('z', Ts);
Hz = (z^2 + z)/(z^2 - 0.5 * z + 0.125)
z^2 + z
z^2 - 0.5 z + 0.125
Sample time: 1 seconds
Discrete-time transfer function.
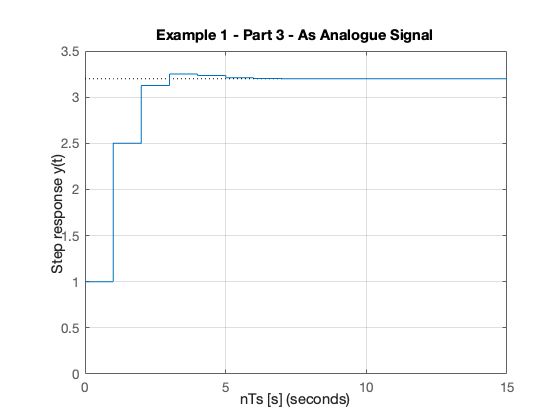
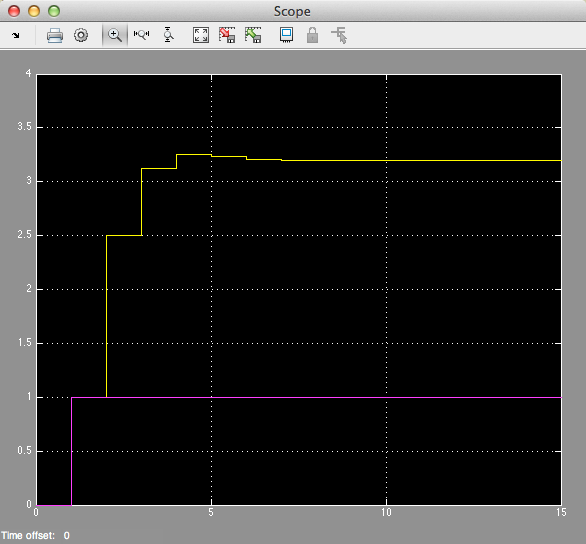
step(Hz) grid title('Example 1 - Part 3 - As Analogue Signal') xlabel('nTs [s]') ylabel('Step response y(t)') axis([0,15,0,3.5])
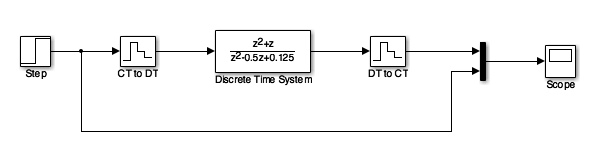
In analogue electronics, to implement a filter we would need to resort to op-amp circuits with resistors, capacitors and inductors acting as energy dissipation, storage and release devices.
To achieve this, all we need is to be able to do is to sample and process the signals quickly enough to avoid violating Nyquist-Shannon’s sampling theorem.
Let’s see what the help function says:
help c2d
C2D Converts continuous-time dynamic system to discrete time. SYSD = C2D(SYSC,TS,METHOD) computes a discrete-time model SYSD with sample time TS that approximates the continuous-time model SYSC. The string METHOD selects the discretization method among the following: 'zoh' Zero-order hold on the inputs 'foh' Linear interpolation of inputs 'impulse' Impulse-invariant discretization 'tustin' Bilinear (Tustin) approximation. 'matched' Matched pole-zero method (for SISO systems only). 'least-squares' Least-squares minimization of the error between frequency responses of the continuous and discrete systems (for SISO systems only). 'damped' Damped Tustin approximation based on TRBDF2 formula (sparse models only). The default is 'zoh' when METHOD is omitted. The sample time TS should be specified in the time units of SYSC (see "Tim
eUnit" property). C2D(SYSC,TS,OPTIONS) gives access to additional discretization options. Use C2DOPTIONS to create and configure the option set OPTIONS. For example, you can specify a prewarping frequency for the Tustin method by: opt = c2dOptions('Method','tustin','PrewarpFrequency',.5); sysd = c2d(sysc,.1,opt); For state-space models, [SYSD,G] = C2D(SYSC,Ts,METHOD) also returns the matrix G mapping the states xc(t) of SYSC to the states xd[k] of SYSD: xd[k] = G * [xc(k*Ts) ; u[k]] Given an initial condition x0 for SYSC and an initial input value u0=u(0), the equivalent initial condition for SYSD is (assuming u(t)=0 for t<0): xd[0] = G * [x0;u0] . For gridded LTV/LPV models (see ssInterpolant), C2D discretizes the LTI model at each grid point and interpolates the resulting discrete-time data. To interpolate the continuous-time data instead, first convert the gridded model to LTVSS or LPVSS. For all other LTV/LPV mode
ls, C2D uses the Tustin method which amounts to fixed-step integration with the trapezoidal rule. See also C2DOPTIONS, D2C, D2D, SSINTERPOLANT, LTVSS, LPVSS, DYNAMICSYSTEM. Documentation for c2d doc c2d Other uses of c2d DynamicSystem/c2d ltipack.tfdata/c2d
doc c2d
First determine the cut-off frequency \(\omega_c\)
\[\omega_c = 2\pi f_c = 2\times \pi \times 20\times 10^3\;\mathrmwc = 2*pi*20e3